深度学习阅读01

深度学习阅读01

第二章 线性代数

标量、向量、矩阵与张量

1. 标量（scalar）是一个单独的数字
2. 向量（vector）是一组数字
3. 矩阵（matrix）为二维的向量
4. 张量（tensor）为多维矩阵

矩阵乘法

1. 定义略
2. 性质如下

单位矩阵和逆矩阵

1. 单位矩阵的定义类似于群论中的幺元，任何矩阵与单位矩阵相乘后仍为自身。即单位矩阵的主对角线应该全为1，其他为0。
2. 矩阵$A$ 的逆矩阵记为$A^{-1}$ ，满足$AA^{-1}=A^{-1}A=I_n$，$n$为矩阵维度

线性相关和生成子空间

对于线性方程组$Ax=b$，如果逆矩阵$A^{-1}$存在，那么必然存在一个唯一的解$x=A^{-1}b$。

为了分析该方程组有多少解，我们将矩阵$A$看作是列向量的组合，即$A={A_!.A_2,A_3,…,A_n}$，那么方程可写为$\Sigma x_iA_i=b$。

我们将这些向量放在$\mathbb{R}^n$的空间中，那么我们需要去选择如何组合这些向量，来使得可以从原点出发，在这些向量的方向上运动后达到$b$。这种操作称为线性组合。我们称一组向量的生成子空间为原始向量经过线性组合后能达到的所有点的集合。

同时，和矩阵的秩联系在一起，如果某个维度上，这些向量的值全为0，那么不可能通过线性组合组合出目标向量$b$。这也恰好说明了此时矩阵不满秩。

范数

我们需要衡量向量的大小，一般地，我们使用称为范数（norm）的函数来衡量向量大小，形式上，$L^p$范数定义如下 $||x||_p=(\Sigma|x_i|^p)^{\frac{1}{p}}$ 从直观上来讲，向量$x$的范数衡量远点到点$x$的距离。

更严谨地，范数是满足以下性质的任意向量函数

• $f(\boldsymbol{x})=0=>\boldsymbol{x}=0$
• $f(\boldsymbol{x}+\boldsymbol{y}) \leq f(\boldsymbol{x}) + f(\boldsymbol{y})$
• 

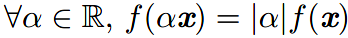
$p=2$时，$L^2$称为欧几里得范数。

有时候我们会希望衡量矩阵的大小，此时我们会使用Frobenius 范数 $||\boldsymbol{A}||_F=\sqrt{\Sigma A^{2}_{i,j}}$

特殊类型的矩阵和向量

• 对角矩阵：对角线上非零，其他为0，可表示为$diag(\boldsymbol{v})$，意为由向量$v$组成的对角矩阵，换而言之，$diag(\boldsymbol{v})\boldsymbol{x}=\boldsymbol{v} \bigodot\boldsymbol{x}$
• 对称，转置后与自身相等
• 正交矩阵：$\boldsymbol A^T\boldsymbol A=\boldsymbol A \boldsymbol A^T=\boldsymbol I$

• Previous
  Floyd快慢指针算法
• Next
  NLP学习：RNN Encoder and Decoder with Attention